Mars en décembre
La série des occultations planétaires par la Lune est en plein essor en cette année 2022. Après la première saison impliquant Uranus (voir la Lettre d’information de l’IMCCE d’octobre 2022), voici maintenant la seconde saison dont l’acteur principal sera la planète Mars.
Au petit matin du 8 décembre, la planète rouge va ainsi disparaître des cieux, en apparence, pendant un peu moins d’une heure, cachée qu’elle sera par le disque lunaire.
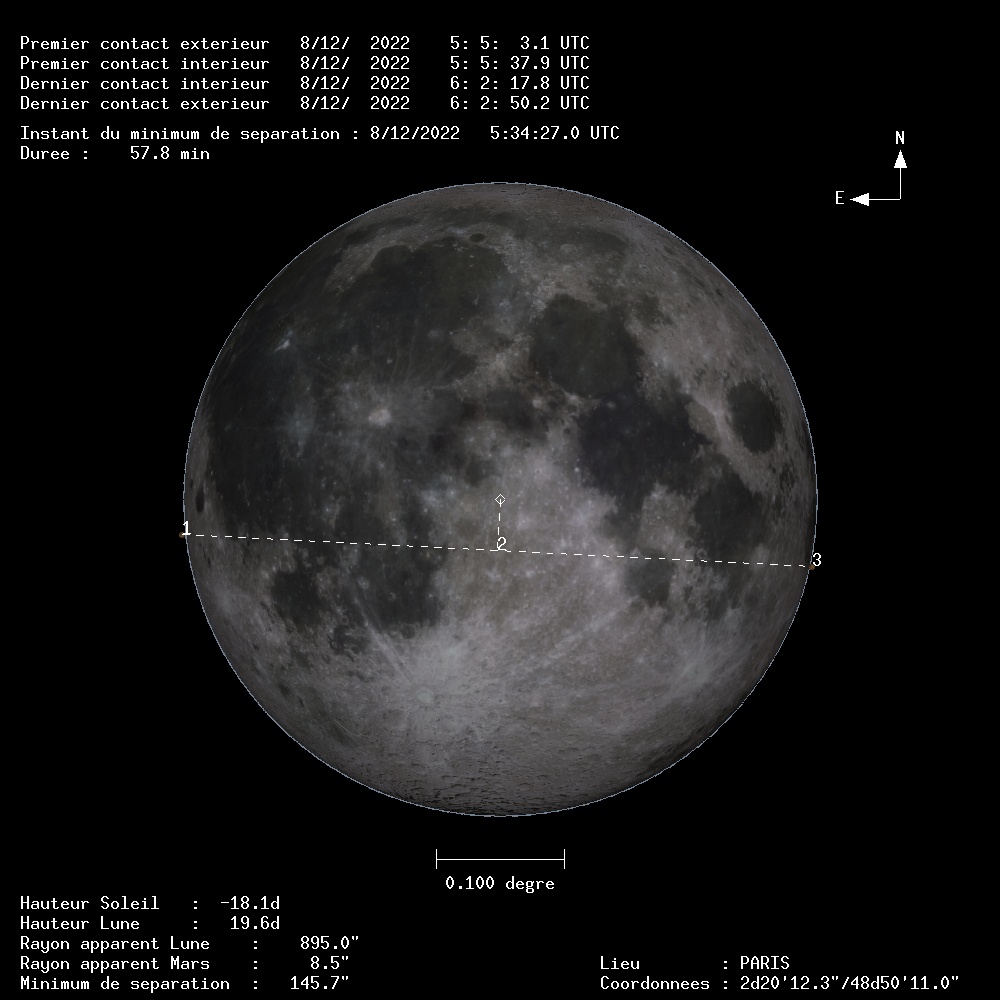
Le phénomène en lui-même est exceptionnel à plus d’un titre.
Côté Mars pour commencer, la planète sera à son opposition précisément durant le temps de son occultation. À l’opposition, l’angle formé par les directions Terre-Mars et Terre-Soleil est de 180°. En d’autres termes, lorsque vous regarderez la Lune et Mars à cet instant, le Soleil sera exactement dans le dos selon une position diamétralement opposée.
L’instant de l’opposition de Mars surviendra ce 8 décembre 2022 à 5 h 41 min UTC (Temps universel coordonné, ajouter une heure pour obtenir le Temps légal français). Cela signifie que Mars sera proche de sa brillance maximale avec une magnitude visuelle de − 1,87, mais aussi que sa taille apparente angulaire sera substantielle, soit 17 secondes de degré.
Le phénomène – la disparition, puis la réapparition de Mars derrière le limbe lunaire – sera donc particulièrement facile à observer à l’œil nu. Dans son mouvement apparent, vu depuis la Terre, Mars sera dans cette boucle artificielle qu’elle décrit dans le ciel depuis le 31 octobre à l’approche de chaque opposition (tous les 2,13 ans), donnant l’impression de rebrousser chemin – on parle de « mouvement rétrograde » – avant de reprendre sa course normale à travers les constellations du Zodiaque.
Concernant la Lune, Mars étant à son opposition, il en sera de même de la Lune, dans ce cas-là, on parle de « pleine lune ». Le disque lunaire sera éclairé sur presque toute sa surface par la lumière du Soleil qui, en France, sera encore sous l’horizon est proche de son lever.
La Lune sera à une position de son orbite située entre deux lieux remarquables, d’une part son nœud ascendant – lieu d’intersection de son orbite avec le plan de l’écliptique qui est le plan contenant le Soleil et la Terre (orbite terrestre) – par lequel elle sera passée quelques jours plus tôt (le 5 décembre) et d’autre part son apogée lunaire – lieu de l’orbite le plus éloigné de la Terre – qu’elle atteindra le 12 décembre. La proximité avec le nœud permet la possibilité d’une occultation, tandis que celle avec son apogée occasionne un déplacement apparent de la Lune plus lent et une taille apparente plus petite, tout l’inverse d’une super Lune !
Nous aurons donc un super phénomène pour une super mini-Lune.
Si le phénomène de décembre va principalement être un spectacle offert aux métropolitains, cependant, dans l’hémisphère sud, une session de rattrapage sera proposée du côté de l’océan Indien le 3 janvier prochain. Mars la rouge sera certes un peu moins brillante et un peu plus petite – nous serons près d’un mois après l’opposition, mais ceci sera compensée par une Lune non pleine qui offrira son bord sombre à l’immersion de la planète, rendant ainsi le phénomène beaucoup plus visible et donc spectaculaire. L’occultation sera également beaucoup moins centrale, la datation précise de ses principaux instants de contact sera donc une donnée qui sera intéressante à comparer aux prédictions.
En effet, les instants issus du calcul sont obtenus à partir d’une forme de la Lune parfaitement sphérique. La Lune n’est bien évidemment pas une sphère parfaite.
D’une part sa surface montre un relief formé de cratères et de montagnes. Les sommets des montagnes lunaires culminent entre 1 500 m et 3 000 m. Cela se traduit par un profil du limbe lunaire irrégulier, parsemé de pics et de vallées. Si Mars, lors de son immersion derrière le bord lunaire, rencontre l’un de ces pics ou une de ces vallées, cela peut modifier la datation de ce contact de plusieurs secondes. En effet, le mouvement relatif moyen de Mars est de 0,5″/s : à cette vitesse, le temps mis par Mars pour parcourir une distance équivalente à celle d’une montagne lunaire de 3 km d’altitude – sachant que la Lune d’un diamètre moyen de 3 474 km présente une taille angulaire apparente de l’ordre de 30″ – sera de 1,5 s.
D’autre part, tout comme la Terre, la Lune présente un léger aplatissement au niveau de ses pôles. Cet aplatissement peut se traduire par de très petits décalages dans les instants de contact observés, même dans le cas d’une lune parfaitement lisse. Cet effet est cependant plus petit que celui provoqué par le relief lunaire, mais doit être en revanche quasiment identique entre les phases d’immersion et d’émersion, puisqu’il est indépendant du relief lunaire, ce qui permet de le discriminer.
Enfin, les conditions d’observations, c’est-à-dire les instants et les positions des contacts, dépendent des lieux d’observation.

Vous avez dit occultation ?
Pour commencer, révisez vos bases en vous exerçant sur le module interactif suivant.
L’observation d’occultations planétaires par la Lune a toujours eu cours depuis l’Antiquité. Seuls les Babyloniens, et dans une moindre mesure les astronomes grecs, ont enregistré ces phénomènes de façon régulière.
À l’époque médiévale, ceci était particulièrement vrai pour les civilisations asiatiques (Chine, Corée et Japon), mais beaucoup moins du côté européen où elles revêtent un caractère anecdotique.
Avec l’avènement du télescope (xviie siècle) et la naissance de l’astronomie moderne, les observations deviennent systématiques à portée scientifique. Le but principal est d’améliorer la théorie du mouvement de la Lune par la datation précise des instants d’immersion et d’émersion des planètes ou étoiles derrière le limbe lunaire. Les quelques datations de l’ère prétélescopique sont très imprécises du fait de la très grande difficulté à dater à l’œil nu l’instant précis auquel une planète (ou une étoile) disparaîtra derrière le limbe lunaire qui délimite la partie éclairée de la Lune, ce qui explique que les occultations observées concernaient en priorité Vénus et, dans une moindre mesure, Jupiter.
Toutefois, les observations anciennes de l’époque médiévale, pour certaines d’entre-elles, conservent un intérêt pour tenter d’estimer le ralentissement de la rotation de la Terre, dont la quantification peut être obtenue par la comparaison de deux échelles de temps, l’une est indépendante de la rotation de la Terre (dénommée TT pour temps terrestre qui est l’échelle de temps utilisée pour le calcul des éphémérides géocentriques et que l’on peut assimiler à une échelle de temps idéale donc pour un écoulement uniforme du temps) et l’autre est définie par la rotation de la Terre (TU pour Temps universel, échelle pour laquelle, par définition, il s’écoule 24 heures entre deux passages du Soleil au méridien d’un même lieu). Cette grandeur est notée ΔT = TT − TU. Par exemple, au 1er janvier 2018, on a ΔT : 69,184 s.
Compte tenu du ralentissement de la rotation de la Terre, mais aussi de l’accélération séculaire de la Lune sur son orbite, l’enregistrement de la datation d’événements dans le passé comparé au calcul donné par l’éphéméride de la Lune permet de déterminer pour chacun d’eux la valeur de ΔT. Par exemple, l’occultation de Jupiter par la Lune du 23 novembre 755, alors que la Lune était éclipsée, apparaît pour la première fois dans les annales de Simeon de Durham qui déclare :
« Le huit des Kalendes de décembre, la Lune âgée de quinze jours, c’est-à-dire à la pleine lune, s’est teintée d’une couleur rouge sang, puis, l’obscurité diminuant peu à peu, elle est revenue à son ancien lustre. En effet, de façon très remarquable, une étoile brillante, qui suivait la Lune elle-même et la traversait, la surpassait en brillance, autant qu’elle était inférieure avant l’obscurcissement de la Lune. »
Cette observation est très célèbre, car c’est la seule de ce type durant une éclipse totale de Lune pendant toute la période médiévale (entre 500 et 1500). Jupiter apparaissait ainsi excessivement brillante comparée à l’éclat de la Lune fortement assombrie durant son passage dans le cône d’ombre de la Terre. Elle était encore commentée au xixe siècle, notamment par Olbers, et fut utilisée récemment pour la mesure du ΔT, qui était alors de l’ordre de 5 000 s.
Les occultations stellaires
Vers le début du xxe siècle, après l’introduction au siècle précédent de la technique photographique comme nouvelle méthode instrumentale d’observation, on s’est aperçu que la Lune pouvait être grandement utile dans la détermination de la taille des étoiles, du moins les plus brillantes susceptibles de se retrouver sur la trajectoire de la Lune.
La méthode consiste à utiliser le corps sombre le plus grand en taille apparente pour mesurer la taille apparente des corps les plus petits du ciel nocturne, les étoiles. En effet, la Lune a une taille apparente (ou diamètre apparent) de l’ordre de 1 800″ (pour rappel, 1 degré contient 3 600″), alors que celle des étoiles est d’environ 0,001″, soit près de deux millions de fois plus petite.
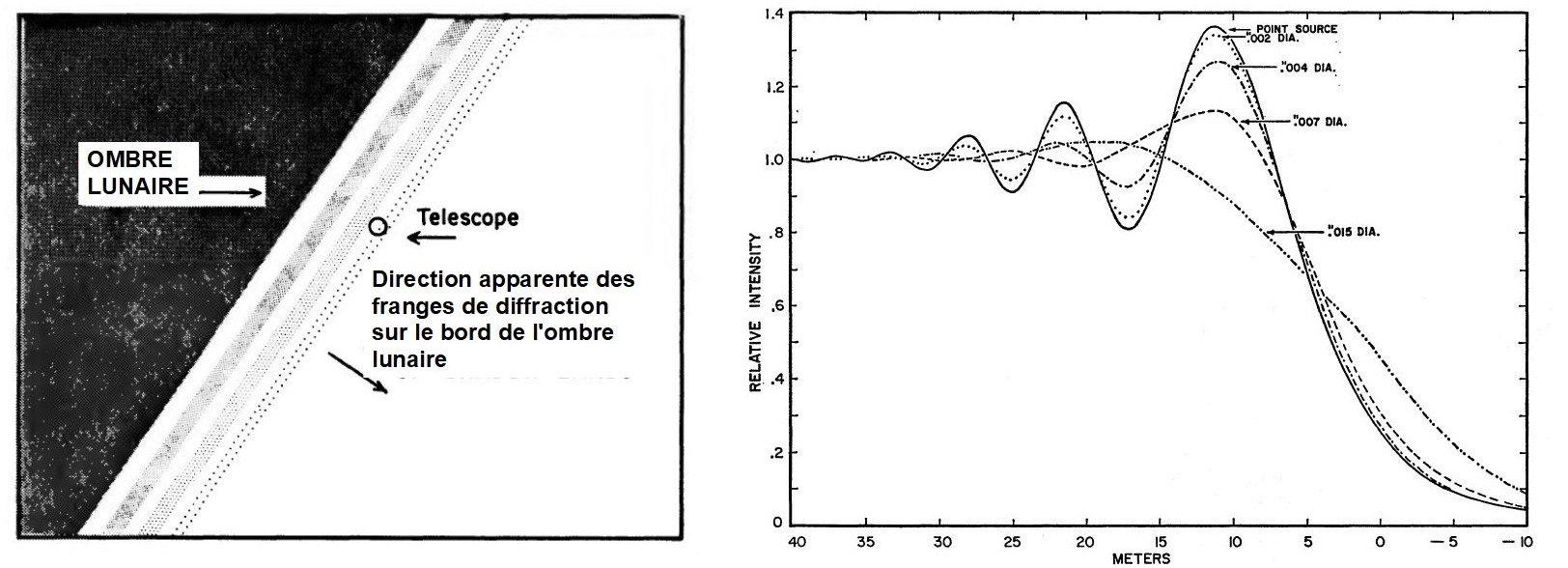
Le principe repose sur la propriété de diffraction de la lumière émise par l’étoile par les obstacles qu’elle rencontre dans sa propagation, en l’occurrence par le bord lunaire. La lumière se comporte à la façon d’une onde, de sorte qu’au passage de l’ombre de la Lune sur Terre (tout comme le Soleil qui occasionne une ombre gigantesque à l’occasion d’une éclipse de Soleil, une étoile, beaucoup plus modestement, fait de même), celle-ci est précédée d’un réseau de franges de diffraction, alternativement sombres et brillantes. Plus la taille de l’étoile augmente, moins les franges sont fines. Ces franges se déplacent sur Terre à une vitesse de 900 mètres par seconde, il est donc nécessaire d’avoir recours à de la photométrie rapide (la photométrie est la mesure de la quantité de lumière reçue dans un télescope), ce que permet la technique photographique. L’une des premières mesures de diamètres stellaires au moyen d’occultations lunaires fut celle de Régulus de la constellation du Lion en 1936, dont la taille fut mesurée à 0,0018″.
Vous avez dit rétrogradation ?
Avant d’atteindre le quasi-alignement Soleil-Terre-Mars au moment de l’opposition, le mouvement apparent de Mars est rétrograde par rapport aux étoiles.
La planète semble d’abord ralentir, puis s’immobilise par rapport à ces dernières. Après cet état suspendu, la planète accélère, puis reprend sa route en sens inverse, c’est-à-dire dans le sens direct.
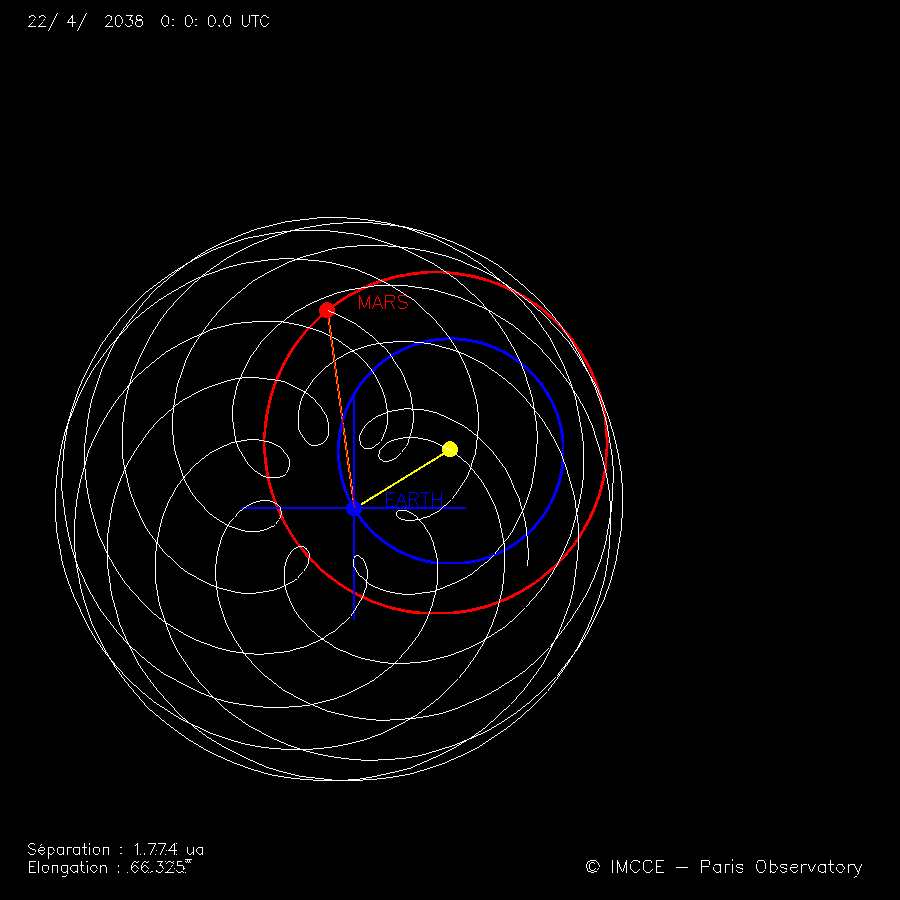
de 16 ans entre le 1er mai 2022 et le 22 avril 2038. Chaque boucle correspond
à une opposition de Mars. Crédits P. Descamps/IMCCE
L’animation présente la boucle apparente décrite au voisinage de l’opposition de décembre 2022 qui engendre alors le zigzag observé. Pourtant, Mars la rouge n’a rien fait d’autre que de continuer à tourner sagement autour de son cher Soleil. La rétrogradation martienne ne peut s’expliquer que dans un univers héliocentrique et non géocentrique. Sur l’animation, les orbites autour du Soleil (en jaune), de la Terre (en bleu) et de Mars (en rouge) sont représentées. À noter la forte excentricité de l’orbite martienne. Le mouvement apparent de Mars par rapport à la Terre décrit une courbe (en blanc) construite simplement en reportant chaque position relative de Mars par rapport au centre de la Terre dans un repère centré sur celui-ci, dont les axes restent fixes dans l’espace, mais dont le centre tourne autour du Soleil. Le repère est dit tournant.
Vue du Soleil, la trajectoire de Mars est quasi-circulaire de centre le Soleil lui-même. Cependant, vue de la Terre, la trajectoire de Mars est très différente, elle est décrite par une série de boucles qui se forment au voisinage d’une opposition. Les oppositions de Mars reviennent tous les 2,13 ans (2 ans et 50 jours). Certaines oppositions sont plus remarquables que d’autres, ce sont les oppositions périhéliques. Elles se produisent au voisinage du passage de Mars par son périhélie. La distance entre la Terre et Mars est alors minimale : 0,372 au. Le périhélie de Mars se trouve à la longitude héliocentrique de 336° qui correspond à la longitude héliocentrique de la Terre atteinte le 27 août. Lors de ces oppositions, les boucles sont très resserrées du fait de la vitesse plus élevée de Mars. Elles se reproduisent tous les 15 ans environ. La prochaine se produira le 15 septembre 2035.
Si l’orbite de Mars était parfaitement circulaire, sa trajectoire serait très proche d’un limaçon de Pascal. La rotation lente de la ligne des oppositions dans le sens inverse des aiguilles d’une montre provient du fait que le rapport des vitesses angulaires de Mars et de la Terre est légèrement supérieur à ½. Si jamais on découvrait sur Mars un limaçon fossilisé, la boucle serait bouclée !
Ptolémée s’était intéressé au limaçon, car très tôt les Grecs avaient été frappés par quelques astres exceptionnels qu’ils appelèrent « planètes » signifiant « astre errant », et dont les trajectoires capricieuses défiguraient le ballet parfaitement réglé des autres corps célestes. En effet, ces « rebelles » décrivent des arabesques au cours desquelles ils s’arrêtent, reviennent en arrière, hésitent à nouveau et repartent enfin dans le sens initial. De tels parcours font penser aux traces incertaines laissées derrière eux par nos paisibles gastéropodes. Voulant expliquer ce comportement étrange, Ptolémée construisit une théorie aussi belle qu’inexacte, dont la complexité est un éloge par défaut de la simplicité. La morale de cette fable, qui aurait pu être une fable de La Fontaine intitulée La Planète et le Limaçon, fut tirée quatorze siècles plus tard par Copernic qui montra que cette valse-hésitation trouve simplement son origine dans la composition de mouvements propres avec celui de notre plateforme d’observation, la Terre.
par Étienne Pascal (1588-1651), le père de Blaise Pascal (1623-1662). Crédits IMCCE
Comment l’observer ?
En raison de son mouvement apparent rétrograde, Mars va en quelque sorte à la rencontre de la Lune qui avance à une vitesse moyenne de 0,5″ par seconde, soit un plus d’un demi-degré par heure, ce qui est l’équivalent de son diamètre angulaire apparent parcouru en une heure. La Lune avance beaucoup plus vite que Mars en apparence, de par sa proximité avec la Terre.
Cependant, en combinant le fait qu’elle sera près de son apogée (avec un mouvement apparent de 0,517″/s) et que Mars sera en mouvement rétrograde (avec une vitesse apparente de 0,017″/s), le mouvement relatif de Mars au moment du phénomène aura une vitesse apparente de 0,534″/s. Compte tenu de la taille apparente de Mars – 17,1″, son temps de disparition/réapparition derrière le limbe lunaire devrait être de l’ordre de 32 s.
Ainsi, chronométrer les durées de disparation et de réapparition de Mars permet d’obtenir une estimation fiable de la mesure de la taille apparente de la planète. Plus l’incertitude sur la durée sera faible, plus l’estimation de sa taille sera précise.
L’observation du phénomène peut se décliner de différentes manières, selon que l’on dispose de matériel d’observation ou non. Pour l’essentiel, cela consiste à déterminer aussi précisément que possible les instants des principaux contacts. Ils sont au nombre de quatre :
- deux lors de la disparition/immersion (premier contact extérieur avec le bord lunaire et instant de disparition) ;
- deux lors de la réapparition/émersion de Mars (instant de la réapparition et dernier contact extérieur avec le bord lunaire).
La mesure de ces instants peut se faire visuellement à l’aide d’un simple chronomètre lors d’une observation visuelle ou au moyen d’un système optique (jumelles, lunette ou télescope). Afin d’obtenir la plus grande précision de mesure possible, il est conseillé de s’entraîner au préalable afin d’estimer son temps de réaction, c’est-à-dire la durée du retard ou de l’anticipation à réagir à un phénomène lumineux donné (disparition ou réapparition d’un point lumineux). Il a été montré que le temps de réaction d’un observateur peu expérimenté peut atteindre 1 à 2 secondes.
Pour une datation plus précise des instants de disparition et de réapparition de Mars, l’utilisation d’une caméra vidéo ou CCD/CMOS couplée à un télescope ou une lunette astronomique est nécessaire. Associée à une synchronisation au temps GPS, elle permet d’obtenir une datation de l’ordre du centième de seconde des instants de contact.
La datation des différents contacts comparée aux prédictions permet d’obtenir des éléments d’information sur le profil du relief lunaire rencontré par la planète lors de son immersion puis de son émersion. Ces informations peuvent ensuite être comparées avec les profils des limbes lunaires obtenus par les mesures d’altimétrie des sondes lunaires (par exemple Kaguya ou LOLA).
Observer l’occultation en direct
L’occultation de Mars par la Lune du 8 décembre 2022 sera retransmise en direct sur la chaîne Youtube de l’Observatoire de Paris, de 5 h 30 à 7 h 30.
Accéder au liveAu programme, la diffusion des images obtenues par des instruments situés à Meudon, Juvisy, Nice et au pic du Midi, et une discussion animée par Gilles Dawidowicz, vice-président de la Société astronomique de France (SAF).
Quelques exercices
Dans tous les exercices proposés, les valeurs sont simplifiées, c’est la méthode que nous souhaitons mettre en lumière et non la précision du résultat.
I. Taille apparente, taille angulaire
La taille apparente, ou taille angulaire ou diamètre apparent ou diamètre angulaire d’un objet vu à distance est la distance angulaire entre ses points extrêmes au point d'observation, c’est-à-dire l’angle entre les droites qui relient les extrémités de l’objet et l’observateur.
.png)
Exercice 1 : calculer la taille apparente de la Lune.
Alpha, l’angle correspondant à la taille apparente, se donne en plusieurs unités et est égal à h/d quand il est exprimé en radian.
La division d’une distance par une distance donne un nombre qui n’a plus de dimension et donc d’unité. Nous obtenons donc une valeur seule, que l’on appelle ici « radian ».
Mais il est bien plus simple et précis, pour se repérer, d’utiliser les degrés dont le symbole est « ° », et ce depuis les Babyloniens, qui ont eu la judicieuse idée de diviser le cercle en 360 parties égales, ou 360 secteurs, dont chaque secteur vaut 1°.
- La circonférence d’un cercle est de 2piR (R pour Rayon du cercle).
- Le cercle trigonométrique est par définition un cercle dont le rayon est égal à 1.
C’est pourquoi, pour obtenir la valeur du radian en ° (et c’est en ° que l’on exprime une taille apparente), on applique alpha (valeur du radian obtenue par le quotient ou rapport h/d) (360° /2pi).
Calculer la taille apparente de la Lune, sachant que :
- Le diamètre de la Lune (h sur le schéma) = 3 474 km
- La distance Terre-Lune (d sur le schéma) = 380 000 km
Cliquez pour obtenir la solution !
- Alpha en radian = h/d = 0,0091
- En ° : alpha = 0,0091 * (360°/2pi) = 0,5°
Exercice 2 : calculer la distance à laquelle placer une pièce de 2 euros pour obtenir la même taille apparente que la Lune.
Il faut alors adopter la valeur de l’angle exprimée en radians.
- H = 25,75 mm
Cliquez pour obtenir la solution !
- D = h/alpha = 2829 mm = 2,82 m
Exercice 3 : calculer la taille apparente de Mars.
- Alpha = h/d
- H = 6779 km
- D = 0,54 au
- 1 au = 150 × 106 km (150 millions de kilomètres)
Cliquez pour obtenir la solution !
- Alpha = 0,0048°
Il existe encore une autre unité en astronomie qui est la seconde d’arc. Pour l’obtenir, on multiplie le ° obtenu par 60 pour avoir les minutes d’arc notées ′ et par 60 à nouveau pour obtenir les secondes d’arc notées ″.
Chaque degré contient 60′, et chaque minute de degré (différente de la minute de temps) contient 60″.
Donner la valeur de la taille apparente de Mars en ″ d’arc.
Cliquez pour obtenir la solution !
- Alpha = 17,3″
Exercice 4 : calculer la distance à laquelle placer une pièce de 2 euros pour obtenir la même taille apparente que Mars.
- H = 25,75 mm
Cliquez pour obtenir la solution !
- D = 307 m
II. Le phénomène en mouvement
Vitesse apparente = distance angulaire apparente parcourue en 1 h.
Exercice 1 : occultation de Mars.
Calculer la durée ΔT de l’occultation de Mars par la Lune, sachant que :
- La Lune a une vitesse apparente V = 0,5″/s, soit 0,5°/h
- Mars a une taille apparente D = 17″
Cliquez pour obtenir la solution !
- V = D/ΔT
- ΔT = D/V
- ΔT = taille apparente de Mars /
vitesse apparente de la Lune - ΔT = 17″ /
0,5″/s = 34 s
Au bout de combien de temps Mars réapparaîtra-t-elle ?
- La Lune a une taille apparente D = 0,5°
Cliquez pour obtenir la solution !
- ΔT = D/V
- ΔT = taille apparente de la Lune /
vitesse apparente de la Lune - ΔT = 0,5° /
0,5°/h - ΔT = 1 h
Exercice 2 : calculer la taille apparente de Mars connaissant la vitesse relative de la Lune par rapport à Mars (0,53″/s) à partir des instants P1 et 01 qui marquent respectivement le début de la disparition de Mars et sa disparition totale.
À Paris :
- P1 : 2022-12-08 05:04:51
- O1 : 2022-12-08 05:05:25
Cliquez pour obtenir la solution !
- D = V ΔT
- ΔT = T(O1) − T(P1) = 34 s
- D = 0,53″/s × 34 s
- D = 18″
Exercice 3 : calculer la taille apparente de la Lune connaissant sa vitesse apparente (0,5″/s) à partir des instants 01 et 04 qui marquent respectivement le début de la disparition totale de Mars et le début de sa réapparition.
À Paris :
- P1 : 2022-12-08 05:04:51
- O1 : 2022-12-08 05:05:25
- M : 2022-12-08 05:34:29
- O4 : 2022-12-08 06:02:27
- P4 : 2022-12-08 06:02:59
Cliquez pour obtenir la solution !
- D = V ΔT
- ΔT = T(O4) − T(O1) = 1 h 03 min = 3780 s
- D = 0,5″/s × 3780 s
- D = 1890″ = 31,5′
- D = 0,525°
Ce résultat n’est pas tout à fait juste, car Mars se meut aussi sur son orbite, en sens inverse au moment de l’occultation. Le calcul de la taille apparente de la Lune doit alors tenir compte de la distance réelle parcourue par Mars au moment du phénomène.
Pour obtenir la taille apparente de la Lune au moment du phénomène, il faut déduire du résultat obtenu précédemment la taille apparente de Mars (DMARS).
- Taille apparente de la Lune : D = 0,525° ou 31,5′
- Vitesse relative de Mars par rapport à la Lune : VMARS = 0,03″/s
- Durée du phénomène : ΔT = 3780 s
Cliquez pour obtenir la solution !
- DMARS = VMARS ΔT
- DMARS = 0,03″/s × 3780 s
- DMARS = 113,4″ = 1,9′
- DLUNE = D − DMARS = 31,5′ − 1,9′ = 29,6′
Exercice 4 : calculer l’instant d’émersion de Mars, sachant que la Lune n’est pas une sphère parfaite.
Lors de l’émersion (et de l’immersion) de Mars derrière le bord lunaire, si une montagne s’y trouve, cela modifie la datation du contact jusqu’à plusieurs secondes.
- Mouvement relatif de Mars : 0,53″/s
- Hauteur de la montagne :
H = 3 km (diamètre de la Lune : 3474 km) - Distance Terre-Lune (d sur le schéma) = 380 000 km
- P4 : 2022-12-08 06:02:59
Rappel :
- Le calcul de la taille apparente d’un objet est :
alpha = h/d exprimé en radian.
Cliquez pour obtenir la solution !
- Taille apparente de la montagne :
DMONT = H/d = 3 /380 000 = 0,000008 radian - DMONT = 0,000008 × (360°/2pi) = 0,0017° = 0,6″
- Durée de l’occultation de Mars par la montagne
= 0,6″ /0,53″/s = 1,1 s - Calcul de l’instant P4 avec la montagne
= T(P4) + 1,1 s - P4 = 06:03:00
III. Retour des oppositions de Mars
On appelle révolution sidérale le temps mis par une planète pour effectuer une révolution complète autour du Soleil par rapport aux étoiles considérées comme fixes.
- La révolution sidérale de la Terre est T = 365,256 360 j
- La révolution sidérale de Mars est M = 686,979 846 j
Au bout de combien de temps reviendra une opposition ?
Il s’agit en fait de déterminer le temps au bout duquel Mars reviendra à une même position par rapport à la Terre et au Soleil.
Cliquez pour obtenir la solution !
- Pendant une durée ΔT, la Terre va donc tourner d’un angle 2π/T et Mars d’un angle 2π/M. La Terre avance donc plus vite sur son orbite que Mars.
- Ainsi, au bout d’un temps ΔT, elle a pris sur Mars une avance angulaire égale à Δθ = (2π/T − 2π/M)ΔT.
- Il faut alors déterminer l’intervalle de temps ΔT tel que Δθ = 2π pour garantir le fait que Mars et la Terre ont bien retrouvé une même position relativement au Soleil.
-
On déduit donc facilement que cela sera au bout d’un temps ΔT = S tel que :
- S est appelée la révolution synodique. Avec les valeurs données de T et M, on obtient la valeur S = 779,936 jours, soit 2,1353 années, ou environ 2 ans et 49 jours.
Cartes et données
Circonstances générales
Les données présentées ci-dessous sont issues du portail web des formulaires de calcul d’éphémérides de l’IMCCE :
Occultation
- Durée : 03:55:20.5
- Élongation au Soleil : 177.71°
Mars
- Magnitude : − 1.87
- Rayon apparent : 0.002°
- Fraction illuminée : 1.000
Lune
- Rayon apparent : 0.252°
- Fraction illuminée : 0.999
par la Lune du 8 décembre 2022. Crédits IMCCE
| Phase | Date UTC | λ | φ |
|---|---|---|---|
| Début de l’occultation générale (P1) | 02:16:31 | – 133°49′00.3″ | 15°46′38.7″ |
| Début de l’occultation totale (O1) | 02:17:07 | – 134°01′34.0″ | 15°53′15.4″ |
| Maximum de l’occultation (M) | 04:14:15 | – 77°48′07.2″ | 60°20′57.9″ |
| Fin de l’occultation totale (O4) | 06:11:14 | 13°01′07.0″ | 33°48′40.4″ |
| Fin de l’occultation générale (P4) | 06:11:51 | 12°47′24.5″ | 33°42′20.3″ |
